DSA Cheatsheet – Time Complexities, Algorithms & Examples for Quick Revision

Introduction

When it comes to coding interviews, competitive programming, or engineering exams, Data Structures and Algorithms (DSA) play a crucial role. Mastering DSA is not just about knowing how to code but also about writing efficient solutions that save time and memory.

In this article, we’ve compiled a comprehensive DSA Cheatsheet that covers:

Time Complexities of common operations.
Popular Algorithms every student must know.
Examples to understand implementation better.
Quick revision tables for exam preparation.

Whether you’re preparing for placements at companies like Google, Microsoft, Amazon, or just brushing up for your university exams, this guide will help you revise faster and smarter.

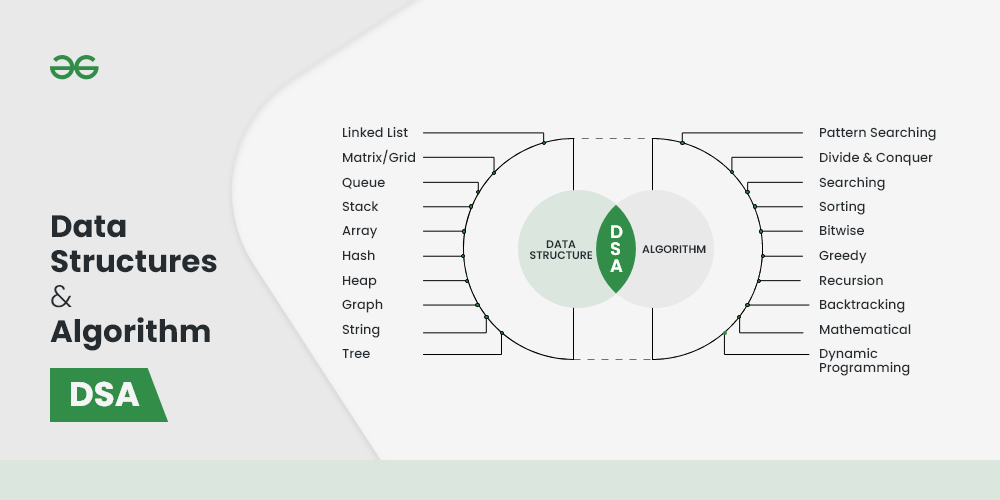
What is DSA and Why is it Important?

DSA (Data Structures and Algorithms) is the backbone of computer science. It helps solve problems efficiently by organizing data properly and applying the right algorithm.

Why DSA Matters:

Exam Success: Most university exams and coding rounds are DSA-heavy.
Placements: 80% of coding interview questions are DSA-based.
Problem-Solving Skills: Improves logical and analytical thinking.
Competitive Edge: Gives you an advantage in hackathons, contests, and coding competitions.

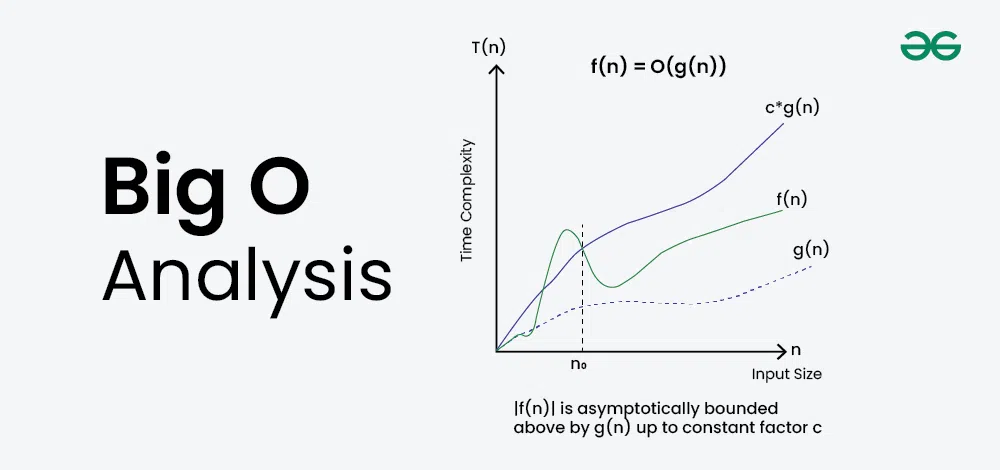
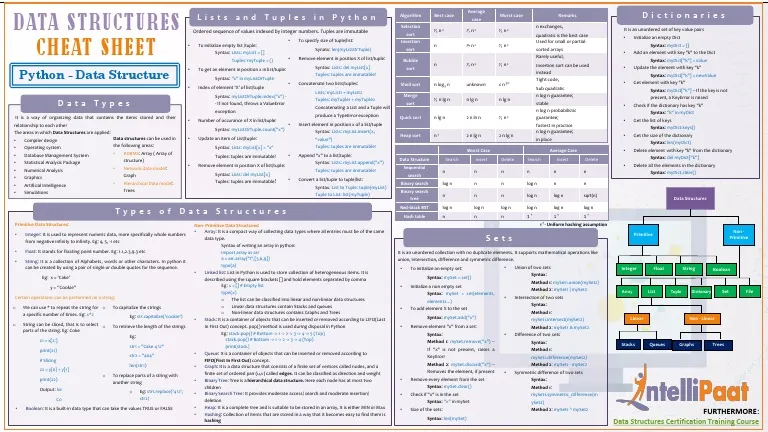
Time Complexity Cheatsheet

One of the most important aspects of DSA is time complexity. Recruiters often ask you to analyze the efficiency of your solution.

Here’s a quick reference table:

Common Time Complexities (Big-O Notation)

O(1): Constant time (e.g., Accessing an array element)
O(log n): Logarithmic (e.g., Binary Search)
O(n): Linear (e.g., Traversing an array)
O(n log n): Log-linear (e.g., Merge Sort, Quick Sort avg. case)
O(n²): Quadratic (e.g., Bubble Sort, Insertion Sort worst case)
O(2^n): Exponential (e.g., Recursive Fibonacci)
O(n!): Factorial (e.g., Traveling Salesman brute force)

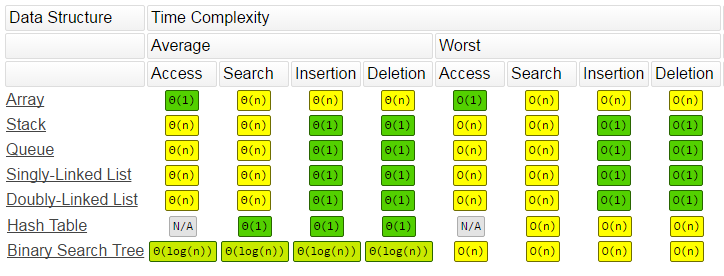
Time Complexities of Common Data Structures

Arrays

Access: O(1)
Search: O(n)
Insert/Delete: O(n)

Linked List

Access: O(n)
Insert at head: O(1)
Delete at head: O(1)

Stack & Queue

Push/Pop/Enqueue/Dequeue: O(1)
Search: O(n)

Hash Table

Search: O(1) average, O(n) worst
Insert/Delete: O(1) average

Binary Search Tree (BST)

Search: O(log n) average, O(n) worst
Insert/Delete: O(log n) average

Must-Know Algorithms in DSA

Let’s break down some of the most frequently asked algorithms in coding interviews and exams.

1. Searching Algorithms

Linear Search: O(n)
Binary Search: O(log n)

2. Sorting Algorithms

Bubble Sort: O(n²)
Insertion Sort: O(n²)
Selection Sort: O(n²)
Merge Sort: O(n log n)
Quick Sort: O(n log n) average, O(n²) worst

3. Graph Algorithms

BFS (Breadth-First Search): O(V + E)
DFS (Depth-First Search): O(V + E)
Dijkstra’s Algorithm: O(V²) or O(E log V) with priority queue
Floyd-Warshall: O(n³)
Kruskal’s Algorithm (MST): O(E log E)

4. Dynamic Programming Algorithms

Fibonacci (DP): O(n)
Longest Common Subsequence (LCS): O(n × m)
Knapsack Problem (0/1): O(n × W)
Matrix Chain Multiplication: O(n³)

Examples of DSA in Coding

Example 1: Binary Search in Python

def binary_search(arr, target):
    left, right = 0, len(arr) - 1
    while left <= right:
        mid = (left + right) // 2
        if arr[mid] == target:
            return mid
        elif arr[mid] < target:
            left = mid + 1
        else:
            right = mid - 1
    return -1

arr = [10, 20, 30, 40, 50]
print(binary_search(arr, 30))  # Output: 2

Example 2: BFS in C++

#include <bits/stdc++.h>
using namespace std;

void bfs(int start, vector<vector<int>>& adj) {
    vector<bool> visited(adj.size(), false);
    queue<int> q;
    q.push(start);
    visited[start] = true;

    while(!q.empty()) {
        int node = q.front(); q.pop();
        cout << node << " ";
        for(auto neighbor : adj[node]) {
            if(!visited[neighbor]) {
                visited[neighbor] = true;
                q.push(neighbor);
            }
        }
    }
}

int main() {
    vector<vector<int>> adj = {{1, 2}, {0, 3}, {0, 3}, {1, 2}};
    bfs(0, adj);
    return 0;
}

Quick Revision Table

Algorithm/Operation	Best Case	Average Case	Worst Case
Linear Search	O(1)	O(n)	O(n)
Binary Search	O(1)	O(log n)	O(log n)
Bubble Sort	O(n)	O(n²)	O(n²)
Merge Sort	O(n log n)	O(n log n)	O(n log n)
Quick Sort	O(n log n)	O(n log n)	O(n²)
BFS/DFS	O(V + E)	O(V + E)	O(V + E)

FAQs About DSA Cheatsheet

Q1. What is the fastest searching algorithm?
Binary Search is the fastest for sorted arrays with O(log n) time.

Q2. Which sorting algorithm is best for competitive programming?
Quick Sort and Merge Sort are commonly used because of O(n log n) efficiency.

Q3. How do I quickly revise DSA before exams?
Focus on time complexities, key algorithms, and coding practice using this cheatsheet.

Q4. Is DSA necessary for placements?
Yes, more than 80% of coding interview questions test your DSA knowledge.

Q5. What is the best way to learn DSA?
Start with arrays and linked lists, then move to stacks, queues, trees, graphs, and dynamic programming.

Conclusion

This DSA Cheatsheet gives you a one-stop solution for quick revision of time complexities, algorithms, and coding examples. Whether you’re preparing for placements, exams, or competitive programming, having this summary will save you time and boost your confidence.

Remember, practice is key — the more problems you solve, the better you’ll understand how and when to apply these concepts.

[CTA BUTTON: Download Free DSA Cheatsheet PDF — Link: https://btechcheatsheets.com/dsa-cheatsheet]

DSA Cheatsheet – Time Complexities, Algorithms & Examples

Introduction